代数方程式:投資への応用

投資の初心者
先生、「代数方程式」って投資とどんな関係があるんですか?よくわからないです。

投資アドバイザー
いい質問だね。たとえば、将来もらえるお金の価値を今のお金の価値に換算する「現在価値」という考え方があるんだけど、それを計算するときに代数方程式を使うんだ。将来のお金の価値をX、現在の価値をYとして、利子率などを組み合わせて方程式を立てて計算するんだよ。

投資の初心者
なるほど。でも、方程式を立てて計算するっていうのが、ちょっと難しそうです。

投資アドバイザー
最初は難しく感じるかもしれないけど、基本的な公式を覚えてしまえば大丈夫だよ。それに、最近は計算ソフトやアプリもあるから、実際に自分で計算する機会は少ないかもしれないね。でも、考え方の基本は代数方程式だから、知っておくと役に立つよ。
代数方程式とは。
投資の話をするときによく出てくる『代数方程式』について説明します。代数方程式というのは、XやYといった文字を使って数を表して計算する式のことです。複数の式を組み合わせて解く連立方程式も同じ仲間です。
はじめに

お金を増やす方法を考える時、多くの人は難しくてよくわからないと感じるかもしれません。将来何が起こるかは誰にもわからず、いろいろなことが複雑に絡み合っていて、まるで迷路のようです。しかし、この複雑な世界を理解するための、中学校や高校で習った強力な道具があります。それは「文字を使った計算式」です。一見、お金の運用とは関係ないように思えるかもしれませんが、文字を使った計算式は、どのような運用をするか決めるために重要な役割を果たしています。
この記事では、文字を使った計算式がお金の運用でどのように役立っているのか、具体的な例を挙げて説明します。例えば、将来お金がどれくらい増えるか計算したい時、「元金×(1+利率)^期間=将来価値」という式が使えます。この式は、今の手持ちのお金が、どれくらいの期間で、どれくらいの利率で増えていくのかを計算するのに役立ちます。また、複数の投資先がある場合、それぞれの利率やリスクを文字で表し、最適な組み合わせを計算することもできます。
さらに、企業の価値を評価する際にも、文字を使った計算式が役立ちます。会社の将来の利益を予測し、それを基に現在の株価が割高か割安かを判断することができます。このように、一見難しく感じるお金の世界も、文字を使った計算式という道具を使うことで、意外と単純でわかりやすい姿が見えてきます。まるで複雑な迷路を解くための地図のように、文字を使った計算式は、お金の運用において、進むべき道を示してくれるのです。この記事を読み進めることで、皆さんがお金の運用をより深く理解し、賢くお金を増やすためのヒントを得られることを願っています。
| お金の計算式 | 用途 | 説明 |
|---|---|---|
| 元金×(1+利率)^期間=将来価値 | 将来価値の計算 | 現在の投資額が将来どれくらいに成長するかを予測 |
| 複数の投資先の利率、リスクを文字で表現 | ポートフォリオ最適化 | 複数の投資先の最適な組み合わせを計算 |
| 将来の利益予測に基づく計算式 | 企業価値評価 | 株価の割安/割高を判断 |
代数方程式とは

数式を用いて未知数の値を探る方法、それが代数方程式です。 未知数は、一般的に X や Y などの記号で表されます。 たとえば、「X に 5 を加えると 10 になる」という文章は、「X + 5 = 10」という代数方程式で表現できます。同様に、「Y の 2 倍から 3 を引くと 7 になる」という文章も「2Y – 3 = 7」という代数方程式で表すことができます。これらの式に含まれる未知数、つまり X や Y の値を解き明かすことが、代数方程式を解くということです。
この代数方程式は、投資の世界でも広く活用されています。 株式投資を例に考えてみましょう。将来の株価は誰にもわかりませんが、過去のデータや市場の動向、企業の業績など様々な要因を考慮することで、ある程度の予測を立てることができます。これらの要因を数式に落とし込み、未知数を将来の株価と仮定することで、代数方程式を構築できます。方程式を解くことで、将来の株価を予測する手がかりを得ることができるのです。
投資収益率の予測にも、代数方程式は役立ちます。 投資額や期間、利率といった様々な要素を数式に組み込み、未知数を投資収益率とすれば、将来の収益を予測する方程式が完成します。もちろん、市場は常に変動するため、これらの予測が必ずしも当たるわけではありません。しかし、複雑な市場の動きを簡潔な数式で表現することで、将来の見通しをある程度定量的に把握し、投資判断の材料とすることができるのです。 つまり、代数方程式は、不確実な投資の世界において、分析や予測を容易にする強力な道具と言えるでしょう。
| 概念 | 説明 | 投資への応用 |
|---|---|---|
| 代数方程式 | 数式を用いて未知数の値を探る方法。未知数は X や Y などの記号で表される。 | 将来の株価や投資収益率の予測に活用される。 |
| 例1 | X + 5 = 10 | 様々な要因を数式に落とし込み、将来の株価を予測する。 |
| 例2 | 2Y – 3 = 7 | 投資額、期間、利率を数式に組み込み、将来の収益を予測する。 |
| 注意点 | 市場は常に変動するため、予測が必ずしも当たるわけではない。 | 予測は投資判断の材料となる。 |
| まとめ | 代数方程式は、不確実な投資の世界において、分析や予測を容易にする強力な道具。 |
投資における活用例

投資の世界では、将来のお金の価値を今の価値に置き換えて考えることがとても大切です。これを「割引現在価値」と言います。たとえば、1年後にもらえる100万円は、今すぐもらえる100万円と同じ価値ではありません。なぜなら、今すぐもらえれば、そのお金を投資に回して利益を得られる可能性があるからです。この将来のお金にどれだけの価値があるのかを計算するのが、割引現在価値の考え方です。
割引現在価値を計算するには、簡単な計算式を使います。将来もらえる金額を「将来価値」、利率を「割引率」、年数を「期間」とすると、「将来価値 ÷ (1+割引率)^期間」で計算できます。例えば、1年後にもらえる100万円を、割引率5%で計算すると、100万円 ÷ (1+0.05)^1 = 約95万2千円となります。つまり、1年後にもらえる100万円は、今の価値に換算すると約95万2千円に相当するというわけです。
この割引現在価値の計算は、様々な投資判断に役立ちます。例えば、複数の投資先を比較する場合を考えてみましょう。それぞれの投資先で将来得られるであろう収益を割引現在価値に換算することで、どの投資先が最も有利かを比較検討できます。また、ある投資案件にどれだけの金額を投資するのが適切かを判断する際にも、割引現在価値の考え方が重要になります。将来得られるであろう収益を割引現在価値に換算し、現在の投資金額と比較することで、その投資案件が魅力的なのかどうかを判断できるのです。このように、割引現在価値は投資を行う上で欠かせないツールと言えるでしょう。
| 用語 | 説明 |
|---|---|
| 割引現在価値 | 将来のお金の価値を現在の価値に置き換えたもの |
| 将来価値 | 将来もらえる金額 |
| 割引率 | 利率 |
| 期間 | 年数 |
| 計算式 | 将来価値 ÷ (1+割引率)^期間 |
| 例 | 1年後にもらえる100万円を、割引率5%で計算すると、約95万2千円 |
| 活用例 | 複数の投資先の比較、適切な投資金額の判断 |
連立方程式とポートフォリオ

複数の式を組み合わせた連立方程式は、投資の世界、特に複数の資産を組み合わせるポートフォリオ作りで重要な役割を担います。投資の世界では、一つの資産だけに全てを託すのではなく、複数の資産を組み合わせてリスクを分散することが一般的です。この際、それぞれの資産の将来の値上がり益に対する期待や、値動きがどれくらい変動するかのリスク、そして資産同士の値動きの関係性を考慮する必要があります。これらの要素を、未知数として連立方程式に組み込むのです。
例えば、二つの資産を組み合わせてポートフォリオを作る場面を考えてみましょう。それぞれの資産の期待収益率、リスク、そしてそれらの間の相関関係を方程式に落とし込みます。さらに、目標とするポートフォリオ全体の収益率を設定します。すると、未知数は各資産への投資比率となり、これを求めることで、目標収益率を達成しつつ、リスクを最小限に抑える最適な資産の組み合わせを見つけることができます。
この考え方は、現代ポートフォリオ理論と呼ばれる投資理論の基礎となっています。現代ポートフォリオ理論は、リスクとリターン(収益)の関係に着目し、効率的なポートフォリオの構築を目指す理論です。数式を用いることで、感覚ではなく、論理的に最適な投資配分を導き出すことができます。
連立方程式は、基本的な二つの資産の組み合わせから、より複雑な多数の資産の組み合わせまで、幅広く応用できます。高度な投資戦略においては、様々な要素を考慮した複雑な連立方程式が使われています。コンピューターの発達により、大量のデータを使った複雑な計算も容易になり、連立方程式は、現代の投資戦略において欠かせない道具となっています。
| 概念 | 説明 | 例 |
|---|---|---|
| 連立方程式の投資への応用 | 複数の資産を組み合わせるポートフォリオ作成において、各資産の期待収益率、リスク、相関関係などを未知数として組み込み、最適な投資比率を計算するために使用される。 | 2資産ポートフォリオにおける最適な投資比率の算出 |
| ポートフォリオのリスク分散 | 一つの資産への集中投資を避け、複数の資産に投資することでリスクを分散する。 | 株式、債券、不動産など異なる資産クラスへの分散投資 |
| 現代ポートフォリオ理論 | リスクとリターン(収益)の関係に着目し、効率的なポートフォリオの構築を目指す理論。連立方程式を用いて最適な投資配分を導き出す。 | 効率的フロンティア |
| 連立方程式の拡張性 | 基本的な2資産ポートフォリオから、多数の資産への応用が可能。 | 多様な資産クラスを含む複雑なポートフォリオの構築 |
| コンピューターと連立方程式 | コンピューターの発達により、大量のデータを用いた複雑な連立方程式の計算が可能になり、高度な投資戦略に活用されている。 | アルゴリズム取引、AIを活用した投資戦略 |
複雑な市場の分析

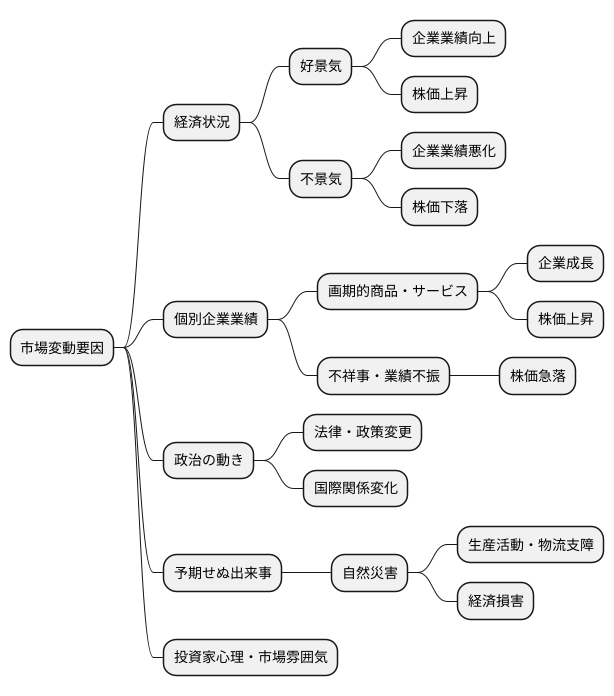
市場は、まるで生き物のように常に変化しています。様々な要因が複雑に絡み合い、予想もつかない動きを見せることが多々あります。経済の状況はその代表的なもので、好景気になれば企業の業績も上がり、株価も上昇する傾向があります。逆に不景気になれば、企業の業績が悪化し、株価も下落する可能性が高くなります。
また、個々の企業の業績も市場に大きな影響を与えます。画期的な新商品やサービスを開発した企業は、急速に成長し、株価も大きく上昇する可能性を秘めています。反対に、不祥事や業績不振に陥った企業は、株価が急落することもあります。
さらに、政治の動きも市場を揺るがす要因となります。新しい法律や政策、国際関係の変化などは、市場に大きな影響を与える可能性があります。予期せぬ出来事、例えば自然災害なども市場に大きな混乱をもたらす可能性があります。地震や台風などの自然災害は、企業の生産活動や物流に支障をきたし、経済全体に大きな損害を与えることがあります。
これらの要因に加え、投資家の心理や市場全体の雰囲気なども市場の動きに影響を与えます。このような複雑に絡み合った要素をすべて考慮に入れて市場を分析することは、人間の力だけでは非常に困難です。そこで、数式を活用することで、これらの複雑な要素をある程度まで式に落とし込み、市場の動きを分析することができます。数式を用いることで、様々な要因が市場に及ぼす影響を数値化し、客観的に分析することが可能になります。もちろん、市場の未来を完全に予測することは不可能ですが、数式を用いることで、より確度の高い分析と予測を行うための助けとすることができます。
まとめ

投資の世界では、一見数学とは無関係に思える様々な要素が複雑に絡み合っています。しかし、その背後には、実は代数方程式という強力な道具が潜んでいるのです。一見すると難解な数式に思えるかもしれませんが、代数方程式は市場の動きを理解し、将来の価格変動を予測するための頼もしい味方となってくれます。
例えば、将来の資産価値を予測する際によく用いられる複利計算は、代数方程式の一種です。現在の資産価値、利率、期間を数式に当てはめることで、将来の資産価値を比較的正確に予測することができます。また、ポートフォリオを最適化する場合にも代数方程式が役立ちます。複数の資産を組み合わせる際、それぞれの資産の期待収益率とリスクを考慮し、最適な配分比率を計算する際に代数方程式が不可欠です。さらに、オプション価格の決定にも代数方程式が用いられています。オプションとは、将来のある時点で、ある価格で株などの資産を買う、あるいは売る権利のことです。この権利の価格を決定する複雑な計算にも、代数方程式が中心的な役割を果たしています。
代数方程式は複雑な市場の動きを分析するための強力なツールと言えるでしょう。市場は様々な要因によって影響を受け、常に変動しています。これらの要因を分析し、将来の市場動向を予測することは容易ではありません。しかし、代数方程式を用いることで、これらの複雑な関係性をモデル化し、より精度の高い予測を行うことが可能になります。ですから、投資の世界に足を踏み入れる際には、代数方程式という強力な道具を積極的に活用することをお勧めします。一見すると敷居が高く感じられるかもしれませんが、その原理を理解し、適切に活用することで、より確かな投資判断を行うことができるはずです。この記事が、皆様の投資活動のより良い理解と成功に少しでも貢献できれば幸いです。
| 投資における代数方程式の活用 |
|---|
| 複利計算による将来資産価値の予測 |
| ポートフォリオの最適化(資産配分比率の計算) |
| オプション価格の決定 |
| 市場分析と将来動向予測 |

