対数の世界:投資への応用

投資の初心者
先生、投資の話で『対数』っていう言葉が出てきたのですが、よく分かりません。大きな数字を指数に置き換えるっていう意味らしいんですけど、どういうことでしょうか?

投資アドバイザー
そうだね。『対数』は、大きな数字を扱いやすくするために使う便利な道具だよ。例えば、100は10の2乗、1000は10の3乗と表せるよね。この時の『2』や『3』が対数にあたるんだ。

投資の初心者
なるほど。100は10の2乗っていうのは分かります。でも、投資でなぜ対数を使う必要があるんですか?

投資アドバイザー
株価の推移など、大きく変化する値をグラフで見やすくするためだよ。対数を使うと、変化の割合を一定の縮尺で表現できるから、長期的な傾向を捉えやすくなるんだ。
対数とは。
『対数』という投資用語について説明します。対数は、とても大きな数を、指数の形に書き換えて、扱いやすくしたものです。
対数とは何か

対数は、大きな数を扱いやすくするための数学的な道具です。莫大な数を比較的小さな数で表すことで、計算や分析を容易にします。具体的には、ある数を基準となる数で何回掛けたら元の数になるのかを表すのが対数です。
例えば、10を2回掛けると100になります。これを対数で表現すると、10を底とする100の対数は2となります。底とは、掛け算の基準となる数のことです。1000は10を3回掛けた数なので、10を底とする1000の対数は3です。このように、対数は掛け算の回数を表していると言えるでしょう。
対数は、様々な分野で活用されています。特に金融の世界では、複利計算や資産価値の評価によく使われます。複利計算とは、利息にも利息が付く計算方法で、時間の経過とともに雪だるま式に資産が増えていく様子を表すのに、対数は非常に役立ちます。また、地震の規模を示すマグニチュードや、音の大きさのデシベルも対数を用いて表現されています。
対数の計算には、いくつかの規則があります。例えば、掛け算は対数の足し算に、割り算は対数の引き算に変換することができます。また、累乗の計算は対数の掛け算として扱うことができます。これらの規則を利用することで、複雑な計算を簡略化することが可能です。
一見複雑に見える対数ですが、底と真数、そして掛け算の回数という関係を理解すれば、それほど難しい概念ではありません。大きな数を扱う様々な場面で、対数は強力な道具となります。
| 項目 | 説明 | 例 |
|---|---|---|
| 対数とは | 大きな数を扱いやすくする数学的道具。ある数を基準となる数で何回掛けたら元の数になるのかを表す。 | |
| 底 | 掛け算の基準となる数。 | 10を底とする100の対数は2(10を2回掛けると100になる) |
| 真数 | 対数を求めたい数。 | 10を底とする100の対数は2(100が真数) |
| 対数の値 | 底を何回掛けたら真数になるかを表す数。 | 10を底とする100の対数は2(2が対数の値) |
| 活用例 | 金融(複利計算、資産価値評価)、地震のマグニチュード、音の大きさ(デシベル) | |
| 計算規則 | 掛け算→対数の足し算、割り算→対数の引き算、累乗→対数の掛け算 |
投資における対数の活用

お金を殖やすための手段として、投資は広く知られています。投資の世界では、複利計算などで対数がよく使われます。複利計算とは、元本に利子が付くだけでなく、その利子にもさらに利子が付く計算方法です。
時間をかければかけるほど、雪だるま式にお金が増えていくのが特徴です。この増え方を表すのに、指数関数というものが使われます。しかし、指数関数で表された数字をそのまま扱うのは難しい場合があります。そこで、対数を使うことで、お金の増え方をより分かりやすく把握できるようになります。
対数は、大きな数字を扱う際に特に役立ちます。例えば、ある商品の値段が100円から200円に上がった場合と、1000円から2000円に上がった場合を比べてみましょう。どちらも値上がり幅は100円ですが、100円から200円への値上がりは元の値段の2倍、1000円から2000円への値上がりは元の値段の1.5倍です。このように、同じ値上がり幅でも、元の値段に対する割合は大きく違います。対数を使うと、この割合の変化を適切に捉えることができます。
また、株価の動きを比較する際にも、対数は力を発揮します。異なる会社の株価を比べる時、単純な値上がり幅や値下がり幅を比較するだけでは不十分です。100円の株が200円になるのと、1000円の株が1100円になるのでは、値上がり幅は同じ100円ですが、元の値段に対する割合は大きく異なります。このような場合、対数を使うことで、それぞれの株価の変動率を正確に比較することができます。
対数は、投資における様々な計算を分かりやすく整理する、便利な道具と言えるでしょう。複利計算における資産の増加率の把握や、株価の変動率の比較など、投資判断を行う上で重要な情報を提供してくれます。投資を行う際には、対数の概念を理解し、活用することで、より効果的な投資判断を行うことができるでしょう。
| 場面 | 問題点 | 対数の利点 |
|---|---|---|
| 複利計算 | 指数関数で表されるお金の増加を把握しにくい | 増加率を分かりやすく把握できる |
| 商品の値上がり | 同じ値上がり幅でも、元の値段に対する割合の違いが分かりにくい | 割合の変化を適切に捉えることができる |
| 株価の比較 | 単純な値上がり/値下がり幅の比較では不十分 | 株価の変動率を正確に比較できる |
対数チャートの読み方

株や為替などの値動きを見る際に、よく使われるのが図表です。図表には、値幅をそのまま表すものと、値動きの割合を表すものがあります。値動きの割合を表す図表は、対数チャートと呼ばれます。
普通の図表では、例えば100円から200円への値上がりと、200円から300円への値上がりは、どちらも100円の差なので、図表上では同じように表されます。しかし、100円から200円への上昇は2倍になっているのに対し、200円から300円への上昇は1.5倍です。値上がり率で考えると、最初の値上がりの方が大きいことが分かります。
対数チャートでは、この値上がり率を同じ間隔で表します。つまり、100円から200円への上昇(2倍)と、200円から400円への上昇(2倍)は、対数チャートでは同じ間隔で表されます。100円から200円への上昇と、200円から300円への上昇を比べると、対数チャートでは前者の方が間隔が大きくなります。このように、対数チャートは値動きの割合を視覚的に捉えやすくする働きがあります。
特に、長期的な値動きを見る際には、対数チャートが役立ちます。長い期間でみると、値上がり幅だけでなく、値上がり率も重要になります。例えば、10年間で株価が100円から200円に上がった銘柄と、1000円から1500円に上がった銘柄があるとします。値上がり幅だけ見ると、後者の方が大きく見えますが、上昇率で考えると前者は2倍であるのに対し、後者は1.5倍です。対数チャートを用いることで、値上がり率に着目した分析が可能になり、長期的な投資判断に役立ちます。
| チャートの種類 | 値の表現 | メリット | 例 |
|---|---|---|---|
| 通常のチャート | 値幅をそのまま表示 | 値動きの大きさを直感的に理解しやすい | 100円→200円の上昇と、200円→300円の上昇はどちらも100円上昇として同じ幅で表示 |
| 対数チャート | 値動きの割合を表示 | 値上がり率を視覚的に捉えやすく、長期的な分析に適している | 100円→200円の上昇(2倍)と200円→400円の上昇(2倍)は同じ幅で表示。100円→200円(2倍)と200円→300円(1.5倍)では前者の幅が大きくなる |
対数正規分布とリスク管理

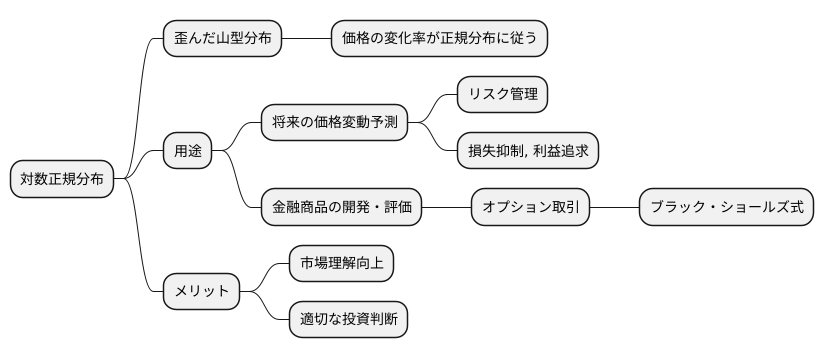
お金にまつわる商品の値段の動きは、よくある山のような形の分布ではなく、歪んだ山のような形の分布に従うことが多いと言われています。これは、値段そのものではなく、値段の変化率(割合)が山のような形の分布に従うと考えるためです。この歪んだ山のような形の分布を、対数正規分布と呼びます。
対数正規分布は、将来の価格変動を確率的に予想するのに役立ちます。例えば、1年後の株価がどのくらいの範囲に収まるのか、あるいはある価格を上回る確率はどのくらいか、といったことを計算することができます。このような予測は、投資におけるリスク管理、つまり損失をできるだけ抑えながら利益を追求するために欠かせないものです。
価格変動の予測は、様々な金融商品の開発や評価にも応用されています。例えば、オプション取引という、将来のある時点で株などの資産をあらかじめ決めた価格で買うまたは売る権利を売買する取引があります。このオプションの価格を計算するための有名な数式として、ブラック・ショールズ式というものがあります。この式は、株価の変動が対数正規分布に従うという前提のもとに作られています。つまり、株価の将来の動きを対数正規分布を使って予測することで、オプションの適正な価格を算出しているのです。
対数正規分布は、金融の世界で広く使われている重要な考え方です。この分布の特性を理解することで、市場の動きをより正確に把握し、適切な投資判断を行うための基礎を築くことができます。
対数の理解で投資判断を向上

お金の世界では、数字の上がり下がりがよく話題になります。例えば、株価が100円から110円に上がれば10円の増加、1000円から1100円に上がれば100円の増加です。同じ10%の増加でも、金額の大きさによって増え方が違って見えます。これが、時として私たちの判断を鈍らせることがあります。
そこで登場するのが「対数」という考え方です。対数は、割合の変化に着目します。100円が110円になるのも、1000円が1100円になるのも、どちらも10%の増加なので、対数で見ると同じ変化として捉えることができます。大きな金額の変化ばかりに目を奪われず、変化の割合を適切に把握できるのです。
株価のチャートを例に考えてみましょう。通常のグラフでは、価格の変化をそのまま線で表します。100円から200円への変化と、1000円から2000円への変化は、同じ2倍でもグラフ上では傾きが違って見えます。一方、対数チャートでは、同じ割合の変化は同じ傾きで表示されます。これにより、異なる価格帯での変化を比較しやすくなります。
また、投資の世界では「対数正規分布」という考え方も重要です。これは、株価や為替などの価格変動が、対数で考えると正規分布に従うというものです。正規分布は、平均値を中心に左右対称に広がる釣鐘型の分布で、統計学でよく使われます。対数正規分布を用いることで、将来の価格変動を確率的に予測することが可能になります。
対数は、最初は少し難しいと感じるかもしれません。しかし、対数を理解することで、市場の動きをより正確に捉え、冷静な投資判断を行うことができます。時間をかけて学ぶ価値は十分にあります。
| 項目 | 通常の考え方 | 対数を使った考え方 |
|---|---|---|
| 価格変動の捉え方 | 金額の増減額に着目 (例: 100円→110円は10円増加) | 変化の割合に着目 (例: 100円→110円は10%増加) |
| チャート表示 | 金額の変化をそのまま表示 (100円→200円と1000円→2000円は傾きが異なる) | 割合の変化を同じ傾きで表示 (100円→200円と1000円→2000円は同じ傾き) |
| 将来価格の予測 | – | 対数正規分布を用いて確率的に予測 |
| メリット | – | 市場の動きを正確に捉え、冷静な投資判断が可能 |
さらなる学習

対数の本質をより深く理解したいと考えるなら、統計学や金融数学といった分野の教科書をひもといてみることをお勧めします。体系的に整理された知識に触れることで、対数の基礎から応用までを段階的に学ぶことができます。大学で使われるような教科書であれば、練習問題も豊富に掲載されているため、理解度を確かめながら学習を進めることができるでしょう。
また、インターネットを活用すれば、様々な情報源から対数に関する知識を無料で入手できます。動画サイトでは、視覚的に分かりやすい解説が多く公開されており、独学で学ぶ際に役立ちます。信頼できるウェブサイトや教育機関が提供するオンライン講座なども、体系的な学習に役立つ貴重な資源と言えるでしょう。さらに、金融に特化した資格試験の教材は、実務的な視点を取り入れながら対数を解説しているため、金融市場における対数の役割について理解を深めるのに役立ちます。
学んだ知識を具体的な場面で活用することも重要です。例えば、チャート分析ツールを使って、株価や為替の動きを対数目盛と通常の目盛で表示し、両者を比較することで、対数目盛の利点や特徴を体感的に理解することができます。実際の市場データを分析する中で、対数がどのように活用されているのか、なぜ重要なのかを理解することで、机上の学習だけでは得られない実践的な知識を身につけることができます。
対数は金融の世界で幅広く活用されています。例えば、投資信託の成長率や債券の利回りなどを計算する際に、対数は必要不可欠な道具となります。また、リスク管理の分野でも、対数は重要な役割を果たします。日々の学習を通して対数への理解を深めることで、金融市場の動向をより正確に把握し、適切な投資判断を行うための礎を築くことができるでしょう。
| 学習方法 | メリット | 具体的な例 |
|---|---|---|
| 統計学・金融数学の教科書 | 体系的な知識、練習問題による理解度確認 | 大学教科書 |
| インターネット | 無料、視覚的に分かりやすい解説、体系的な学習 | 動画サイト、オンライン講座、金融資格試験教材 |
| 実践的な活用 | 体感的な理解、実践的な知識 | チャート分析ツール(対数目盛と通常目盛の比較)、株価・為替の分析 |

