正規分布:投資における活用の基礎

投資の初心者
先生、「正規分布」ってよく聞くんですけど、投資とどう関係しているんですか?

投資アドバイザー
良い質問だね。正規分布は、投資の結果がどんな風にばらつくかを表すのに使われるんだ。例えば、ある投資の平均的な儲けが10%だとしよう。正規分布を使うと、実際の儲けが10%からどれくらい離れるかを確率で考えることができるんだよ。

投資の初心者
なるほど。でも、実際の儲けは誰にもわからないですよね?

投資アドバイザー
その通り。未来のことはわからない。でも、過去のデータから、儲けがどれくらいばらつくか(標準偏差)を計算することができる。正規分布を使うことで、例えば「儲けが5%から15%の間になる確率は68%くらいだ」といった予測ができるんだ。これは投資の判断材料になるんだよ。
正規分布とは。
投資の世界でよく使われる「正規分布」という言葉について説明します。正規分布は、左右対称の釣鐘のような形をした確率の分布のことです。山の頂上が平均値、つまり見込みの収益率を表し、裾野の広がりは標準偏差という値で決まります。この標準偏差が大きいほど、裾野は大きく広がり、逆に小さいほど、裾野は狭くなります。正規分布には、次のような特徴があります。平均値から標準偏差のプラスマイナス1倍の範囲に収まる確率は約68%、プラスマイナス2倍の範囲では約95%、プラスマイナス3倍の範囲では約97%となります。将来の投資は不確実なものですが、この確率分布を用いることで、どのくらいの値が、どのくらいの確率で起こるかをあらかじめ想定することができます。証券投資理論では、この正規分布を前提として考えることが多いです。
正規分布とは

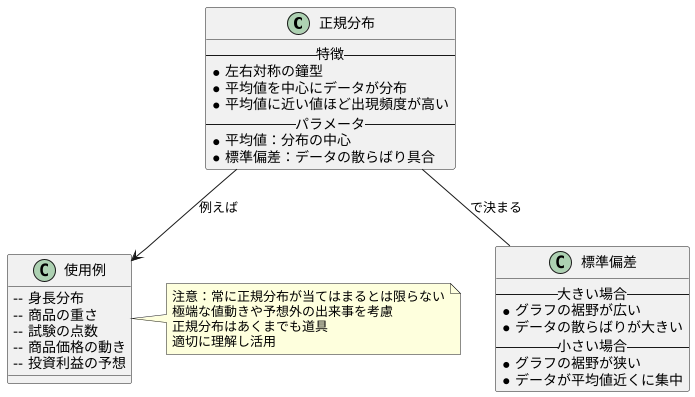
ふつうの分け方として知られる正規分布は、統計の分野で最も大切な考え方の一つであり、お金の動きの世界でも広く使われています。この分け方は、グラフにすると左右同じ形の鐘のような形になるのが特徴です。真ん中の値を中心にデータが散らばり、この鐘の形は、真ん中の値に近い値ほど現れやすく、真ん中の値から離れるほど現れにくいことを示しています。正規分布の形は、平均値と標準偏差という二つの数値で決まります。平均値は分布の真ん中を示し、標準偏差はデータの散らばり具合を示します。
標準偏差が大きい場合は、グラフの裾野が広がり、データの散らばりが大きいことを意味します。反対に標準偏差が小さい場合は、グラフの裾野が狭まり、データが平均値近くに集まっていることを意味します。例えば、たくさんの人の身長の分布は正規分布に従うことが知られています。平均身長に近い人が最も多く、平均から離れるほど人数が少なくなっていくからです。また、商品の重さや試験の点数なども、正規分布に従うことがよくあります。
お金の動きの世界では、例えば、ある商品の価格の動きや、投資による利益の予想などに正規分布が使われます。将来の値動きを鐘の形で表すことで、どの値が現れやすいか、どのくらいの範囲で値が動くのかを予測することができます。ただし、常に正規分布が当てはまるとは限らないため、注意が必要です。極端な値動きや予想外の出来事が起こる可能性も考慮に入れて、慎重に判断することが大切です。正規分布はあくまでも一つの道具であり、それをどう使うかは使う人次第です。適切に理解し、活用することで、より良い結果を得ることができるでしょう。
標準偏差の役割

標準偏差とは、数値の集まりがどれくらい平均値から散らばっているかを示す指標です。これは、投資の世界でリスクを測る物差しとしてよく使われます。標準偏差が高いほど、価格の変動幅が大きく、投資のリスクも高いと考えられます。
例えば、同じように利益が見込める二つの商品があったとします。片方の商品は標準偏差が大きく、もう片方の商品は標準偏差が小さいとします。標準偏差が大きい商品は、価格が大きく上下に変動しやすく、大きな利益を得られる可能性がある一方で、大きな損失を被る可能性も秘めています。つまり、価格の振れ幅が大きい分、不確実性が高く、リスクが高いと言えるのです。
一方、標準偏差が小さい商品は、価格の変動が比較的小さいため、大きな利益は期待できませんが、大きな損失が出る可能性も低いです。価格が安定しているので、リスクは低いと判断できます。
このように、標準偏差を見ることで、投資における価格変動のリスクをある程度予測することができます。しかし、標準偏差は過去のデータに基づいて計算されるため、将来の価格変動を完全に予測できるわけではありません。標準偏差はあくまでもリスクを測るための一つの目安であり、他の要素も総合的に考慮して投資判断を行う必要があります。標準偏差に加えて、投資商品の内容、市場の動向、自分の投資方針なども踏まえて、慎重に検討することが大切です。
また、標準偏差は正規分布しているデータにおいて特に有効な指標となります。正規分布とは、データが平均値を中心に左右対称に分布している状態のことです。投資の世界では、必ずしも全てのデータが正規分布しているとは限らないため、標準偏差だけでリスクを判断するのは危険です。他の統計指標や分析手法も併用することで、より正確なリスク評価を行うことができます。
| 標準偏差 | リスク | リターン | 価格変動 |
|---|---|---|---|
| 高い | 高い | 高くなる可能性も、損失が大きくなる可能性も高い | 大きい |
| 低い | 低い | 大きな利益は期待できないが、大きな損失が出る可能性も低い | 小さい |
注意点:
- 標準偏差は過去のデータに基づいて計算されるため、将来の価格変動を完全に予測できるわけではない。
- 標準偏差はあくまでもリスクを測るための一つの目安であり、他の要素も総合的に考慮して投資判断を行う必要がある。
- 標準偏差は正規分布しているデータにおいて特に有効な指標となる。
確率と正規分布

世の中には偶然性に左右される出来事が数多く存在します。例えば、サイコロを振ってどの目が出るのか、明日の気温は何度になるのかなど、予測が難しい事柄ばかりです。確率論は、このような不確実な事象を扱うための数学的な枠組みです。そして、確率論の中で特に重要な概念の一つが正規分布です。
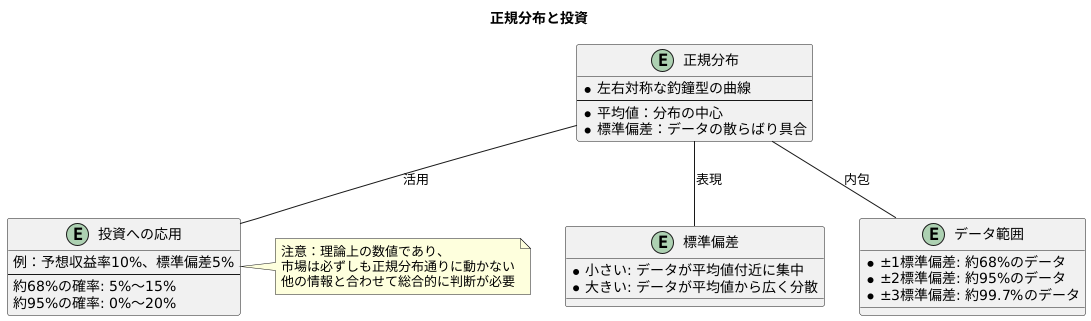
正規分布は、左右対称な釣鐘型の曲線で表され、平均値を中心としたデータのばらつき具合を示すものです。平均値は分布の中心を表し、標準偏差はデータの散らばり具合を表す指標です。標準偏差が小さいほど、データは平均値の近くに集まっており、標準偏差が大きいほど、データは平均値から遠くまで散らばっています。
正規分布においては、平均値からプラスマイナス1標準偏差の範囲に全体の約68%のデータが収まります。プラスマイナス2標準偏差の範囲まで広げると、約95%のデータが収まり、プラスマイナス3標準偏差まで広げると、実に約99.7%ものデータが収まることが分かっています。
この正規分布の性質は、投資の世界でも活用されています。例えば、ある投資商品の予想収益率が10%、標準偏差が5%だとしましょう。この場合、正規分布に基づくと、将来の収益率が5%から15%(平均値±1標準偏差)の範囲に収まる確率は約68%、0%から20%(平均値±2標準偏差)の範囲に収まる確率は約95%と推定できます。つまり、高い確率で収益率がどの範囲に収まるのかを予測することが可能になります。
ただし、これはあくまでも理論上の数値です。現実の市場は複雑な要因が絡み合っており、必ずしも正規分布通りに動くとは限りません。正規分布はあくまでも参考情報として、他の情報と合わせて総合的に判断することが重要です。
投資における活用

お金を育てる世界では、将来の値動きや儲けを正確に言い当てるのは至難の業です。まるで雲の流れを読むように、予測は難しく、確実な答えはありません。しかし、統計学の知恵を借りることで、将来の儲けがある範囲に収まる可能性を推測することができます。その便利な道具の一つが「正規分布」と呼ばれるものです。正規分布は、データが平均値を中心に左右対称に広がる釣鐘型のグラフで表されます。
正規分布を使うことで、将来の儲けがどの程度の範囲に収まるかを確率的に見積もることができます。例えば、平均的な儲けが5%で、標準偏差が2%だとします。標準偏差はデータのばらつき具合を表す数値で、標準偏差が小さいほどデータは平均値の近くに集まり、標準偏差が大きいほどデータは平均値から離れて広がります。この場合、正規分布を用いると、将来の儲けが3%から7%(平均値±標準偏差)の範囲に収まる確率は約68%と推定できます。さらに、1%から9%(平均値±標準偏差の2倍)の範囲に収まる確率は約95%と推定できます。
こうした確率に基づいた予測は、投資家がリスクを理解し、自分に合った投資の選択をする上で役立ちます。例えば、損失をできるだけ避けたい慎重な投資家は、標準偏差が小さく、値動きが安定した投資商品を選ぶでしょう。一方、大きな儲けを狙う積極的な投資家は、標準偏差が大きく、値動きが激しい投資商品を選ぶかもしれません。
ただし、正規分布はあくまでも現実を単純化したモデルであり、実際の市場は必ずしもこの通りに動くとは限りません。思いもよらない出来事が起こり、市場が大きく変動することもあります。ですから、正規分布による予測は参考程度に捉え、他の情報も集めて、多角的に検討することが大切です。様々な情報を組み合わせ、慎重に判断することで、より良い投資の選択に繋がるでしょう。
| 概念 | 説明 | 投資への応用 |
|---|---|---|
| 正規分布 | データが平均値を中心に左右対称に広がる釣鐘型のグラフ。将来の儲けがある範囲に収まる可能性を確率的に見積もることができる。 | 確率に基づいた予測で、リスクを理解し、自分に合った投資選択をするのに役立つ。 |
| 平均値 | データの中心的な値。 | 平均的な儲けを表す。 |
| 標準偏差 | データのばらつき具合を表す数値。標準偏差が小さいほどデータは平均値の近くに集まり、標準偏差が大きいほどデータは平均値から離れて広がる。 | 値動きの安定性を示す。慎重な投資家は標準偏差が小さい投資商品、積極的な投資家は標準偏差が大きい投資商品を選ぶ。 |
| 確率 | ある事象が起こる可能性の度合い。正規分布を用いると、儲けがある範囲に収まる確率を推定できる。 | 例:平均値±標準偏差の範囲に収まる確率は約68%、平均値±標準偏差の2倍の範囲に収まる確率は約95%。 |
| 注意点 | 正規分布は現実を単純化したモデルであり、実際の市場は必ずしもこの通りに動くとは限らない。 | 正規分布による予測は参考程度に捉え、他の情報も集めて、多角的に検討することが大切。 |
限界と注意点

正規分布は、投資の世界で広く使われている統計的手法の一つです。平均値と標準偏差という二つの数値でデータの分布を簡潔に表すことができ、将来の価格変動を予測する際などに役立ちます。しかし、正規分布には限界があり、その特性を正しく理解せずに使うと、誤った判断につながる恐れがあります。
正規分布の大きな限界の一つは、極端な値の発生確率を過小評価することです。正規分布は、データの大部分が平均値付近に集中し、平均値から離れるほどデータの数が少なくなることを前提としています。鐘の形をしたグラフで表現されるように、左右対称に裾野が広がっていますが、その裾野は無限には広がっていません。現実の市場では、稀にではありますが、平均値から大きく離れた、予想外の大きな価格変動が起こることがあります。これは「裾の厚い分布」とも言われ、正規分布ではこの「裾野」の部分、つまり極端な事象の発生確率を低く見積もってしまうのです。
また、正規分布は過去のデータに基づいて将来を予測するモデルです。過去のデータが将来もそのまま当てはまるとは限りません。例えば、経済状況の大きな変化や、予期せぬ出来事により、市場の環境は大きく変わることがあります。過去のデータが将来の予測に役立たなくなる可能性も十分に考えられます。つまり、市場環境の変化に正規分布は対応できないのです。
正規分布はあくまで一つのツールであり、それだけに頼ると思わぬ落とし穴に陥る可能性があります。他の統計的手法や、市場の状況を総合的に判断するなど、多角的な分析をすることで、より精度の高い投資判断を行うことができるでしょう。
| 項目 | 内容 |
|---|---|
| 定義 | 平均値と標準偏差でデータの分布を表す統計的手法。将来の価格変動予測などに役立つ。 |
| メリット | データの分布を簡潔に表現できる。 |
| 限界1 | 極端な値の発生確率を過小評価する(裾の厚い分布への対応不足)。 |
| 限界2 | 過去のデータに基づいており、市場環境の変化に対応できない。 |
| 注意点 | 正規分布だけに頼らず、他の統計的手法や市場状況も考慮した多角的な分析が必要。 |
まとめ

投資の世界では、将来の値動きを正確に言い当てることはできません。しかし、過去のデータから将来をある程度推測することは可能です。その際に役立つのが正規分布という考え方です。正規分布は、平均値と標準偏差という二つの数値で、データのばらつき具合を表す鐘の形をしたグラフです。
正規分布を使うことで、例えばある投資商品の将来の収益率がどの範囲に収まる可能性が高いかを確率的に示すことができます。平均値に近い値ほど出現する確率が高く、平均値から離れるほど確率は低くなります。標準偏差は、データが平均値からどれくらいばらついているかを示す指標です。標準偏差が大きいほど、データのばらつきが大きく、将来の収益率の範囲も広くなります。つまり、不確実性が高いことを意味します。投資家は、この正規分布を用いることで、投資のリスクとリターンをより具体的に理解し、より適切な投資判断を行うことができます。
しかし、正規分布は万能ではありません。現実の市場は常に変化しており、過去のデータが将来もそのまま当てはまるとは限りません。特に、リーマンショックのような大きな出来事、いわゆる「まれな事象」は、正規分布では予測が難しいものです。正規分布は、このような極端な値の発生確率を低く見積もる傾向があるため、リスクを過小評価してしまう可能性があります。また、市場の状況が大きく変化した場合、過去のデータに基づいた正規分布は役に立たなくなる可能性もあります。
したがって、投資判断を行う際には、正規分布の限界を理解しておくことが重要です。正規分布だけに頼るのではなく、他の分析方法も組み合わせて、多角的に情報を分析し、慎重に判断する必要があります。常に市場の変化に注意を払い、柔軟に対応していくことが、投資で成功するための鍵となります。
| 概念 | 説明 | メリット | デメリット |
|---|---|---|---|
| 正規分布 | 平均値と標準偏差でデータのばらつき具合を表す鐘の形をしたグラフ | 将来の収益率の範囲や確率を予測できる。リスクとリターンを具体的に理解できる。 | まれな事象を予測できない。リスクを過小評価する可能性がある。市場の大きな変化に対応できない。 |

