モンテカルロ・シミュレーション:未来予測への活用

投資の初心者
先生、モンテカルロ・シミュレーションって難しそうでよくわからないのですが、簡単に説明してもらえますか?

投資アドバイザー
そうだね、難しく感じるかもしれないけど、簡単に言うと、たくさんの仮想の未来を作って、どうなるかを何度も試す方法だよ。例えば、サイコロを何回も振って、どの目が出やすいかを調べるようなものだね。

投資の初心者
サイコロを振るように、でたらめに試すということですか?でも、投資の予測に、でたらめな方法で大丈夫なのでしょうか?

投資アドバイザー
でたらめだけど、全く規則性がないわけではないんだ。株価や金利の過去の動きや、経済の予想などを考えて、ある範囲内ででたらめに値を決めて計算する。これを何千回、何万回と繰り返すことで、投資の結果がどうなるかを大まかに予測できるんだよ。未来を確実に知ることはできないけれど、起こりうる結果を幅広く知ることができるんだ。
モンテカルロ・シミュレーションとは。
『モンテカルロ・シミュレーション』という投資用語について説明します。この手法はもともと理科や工学の分野で使われていて、式が複雑すぎて解けない問題に、何度もでたらめな実験を繰り返すことで、おおよその答えを出す方法です。年金のお財産管理の予測で使う場合、将来の資産の値動きが予測しづらいので、あらかじめ決めた条件に基づいてでたらめに作った値を使い、何千回、何万回も試行を繰り返すことで、将来の見積もりをします。
手法の由来

モンテカルロ・シミュレーションは、複雑な数式を解くことが難しい科学技術の分野で生まれた手法です。その名前は、カジノで有名なモナコ公国のモンテカルロに由来します。ルーレットのように偶然に左右される実験を何度も繰り返すことで、真の答えに限りなく近いおおよその答えを見つけ出す、という考え方が基礎となっています。
この手法が生まれた背景には、従来の方法では解を求めるのが非常に困難な問題が存在していたという事情があります。例えば、ミサイルの軌道予測や原子炉の設計など、複雑な要素が絡み合い、数式で正確に表すことが難しい現象を扱う必要がありました。このような問題に対して、モンテカルロ・シミュレーションは画期的な解決策を提供しました。数式を直接解くのではなく、乱数を利用して何度も試行を繰り返すことで、求める値の範囲を絞り込んでいくのです。
モンテカルロ・シミュレーションは、ルーレットのように確率に基づいた実験を多数回行うことで、全体的な傾向を把握します。例えば、サイコロを何度も振って出た目の平均値を求めると、試行回数が増えるほど理論上の平均値である3.5に近づいていきます。これと同じように、複雑な現象でも、乱数を用いてシミュレーションを繰り返すことで、真の値に近づくことができます。
現在では、この手法は科学技術の分野だけでなく、金融や経済、経営など、様々な分野で応用されています。例えば、金融商品開発やリスク管理、将来の経済予測など、不確実性が高い状況における意思決定を支援するために活用されています。モンテカルロ・シミュレーションは、複雑な問題を扱う上で強力な道具となり、様々な分野でその力を発揮しています。
| 項目 | 内容 |
|---|---|
| 手法名 | モンテカルロ・シミュレーション |
| 由来 | モナコ公国のモンテカルロ(カジノで有名) |
| 原理 | 偶然に左右される実験を何度も繰り返すことで、真の答えに近いおおよその答えを見つけ出す |
| 生まれた背景 | ミサイルの軌道予測や原子炉の設計など、複雑な数式を解くことが難しい問題に対処するため |
| 解決策 | 数式を直接解くのではなく、乱数を利用した試行を繰り返すことで値の範囲を絞り込む |
| 例 | サイコロを何度も振って出た目の平均値を求める(試行回数が増えるほど3.5に近づく) |
| 応用分野 | 科学技術、金融、経済、経営など |
| 活用例 | 金融商品開発、リスク管理、将来の経済予測など |
金融分野での活用

お金の世界では、モンテカルロ・シミュレーションはとても役に立つ方法です。特に、危険を管理したり、投資の作戦を立てたりする時に力を発揮します。未来の市場の動きや景気を予想するのは至難の業ですが、この方法を使えば、色々な場合を考えて、それぞれの結果を計算できます。
例えば、株や債券の値段の上がり下がり、為替の変動などを、偶然に起こるものとして作り出し、資産全体の価値がどう変わるかを真似てみます。そうすることで、危険と利益の関係をより深く理解できます。未来を完全に知ることはできませんが、色々な可能性を考えると、落ち着いて対応できるようになります。まるで、色々な未来を体験する訓練をしているようです。
この方法は、複雑なお金の商品の価値を調べる時にも使われます。例えば、オプション取引の値段を決める時などです。オプション取引とは、ある値段で株などを買う権利や売る権利を売買する取引のことです。この権利の値段は、将来の株価の予想によって変わります。モンテカルロ・シミュレーションを使えば、色々な株価の動きを想定して、権利の値段を計算することができます。
このように、モンテカルロ・シミュレーションは、色々な場面で使われています。たくさんの計算を繰り返すことで、複雑な問題を解くことができます。まるで、たくさんの小さな試行錯誤を繰り返して、最適な答えを探すようなものです。金融の世界では、この手法を使って、より良い判断ができるように努力しています。未来を正確に予測することはできませんが、起こりうる様々な状況を想定することで、リスクを減らし、利益を最大にするための最善の行動を選択することができるのです。
| モンテカルロ・シミュレーションの用途 | 説明 | 利点 |
|---|---|---|
| リスク管理と投資戦略 | 市場の動きや景気の様々なシナリオを想定し、資産価値の変化をシミュレートする。 | リスクとリターンの関係を深く理解し、適切な対応策を立てることができる。 |
| 複雑な金融商品の評価 | オプション取引などの価格決定に利用。様々な市場変数を想定し、商品の価値を計算。 | 複雑な商品の価格をより正確に算出できる。 |
年金財政における活用

年金財政は、将来世代への給付を確実にするため、長期的な視点に立った慎重な運営が求められます。将来の年金資産の運用収益や受給者の寿命は不確定な要素が多く、従来の手法では正確な財政予測を行うことが困難です。そこで、様々な不確定要素を考慮したシミュレーション手法であるモンテカルロ・シミュレーションが活用されています。
モンテカルロ・シミュレーションは、乱数を用いて様々な経済シナリオを生成し、それぞれの場合における年金基金の資産残高を試算します。例えば、経済成長率、物価上昇率、運用利回り、平均寿命といった変数を乱数に基づいて変化させ、何万通りもの仮想的な未来を描き出します。それぞれの未来において、年金基金の収入(運用収益や保険料収入)と支出(年金給付)を計算し、最終的な資産残高を算出します。
こうして得られた膨大な数のシミュレーション結果を分析することで、年金制度の持続可能性を確率的に評価することができます。例えば、1万回のシミュレーションのうち、9000回で年金基金の資産が枯渇しなかったとすると、年金制度が将来にわたって給付を続けることができる確率は90%と推定できます。また、シミュレーション結果を分析することで、年金制度の脆弱性を明らかにすることも可能です。もし、特定の経済状況下で年金基金が枯渇しやすいことが分かれば、事前に対策を講じることができます。
このように、モンテカルロ・シミュレーションは、複雑な年金財政の将来予測を可能にし、年金制度の持続可能性を評価するための重要なツールとなっています。将来の年金受給者の不安を軽減し、安心して老後を迎えられる社会の実現に貢献しています。
| モンテカルロ・シミュレーションとは | 目的 | 方法 | 評価 | 効果 |
|---|---|---|---|---|
| 乱数を用いて様々な経済シナリオを生成し、それぞれの場合における年金基金の資産残高を試算するシミュレーション手法。 | 年金財政の将来予測、年金制度の持続可能性の評価 | 経済成長率、物価上昇率、運用利回り、平均寿命といった変数を乱数に基づいて変化させ、何万通りもの仮想的な未来を描き出す。それぞれの未来において、年金基金の収入と支出を計算し、最終的な資産残高を算出する。 | 膨大な数のシミュレーション結果を分析することで、年金制度の持続可能性を確率的に評価する。例えば、1万回のシミュレーションのうち、9000回で年金基金の資産が枯渇しなかったとすると、年金制度が将来にわたって給付を続けることができる確率は90%と推定できる。また、シミュレーション結果を分析することで、年金制度の脆弱性を明らかにすることも可能。 | 複雑な年金財政の将来予測を可能にし、年金制度の持続可能性を評価するための重要なツール。将来の年金受給者の不安を軽減し、安心して老後を迎えられる社会の実現に貢献。 |
手法の仕組み

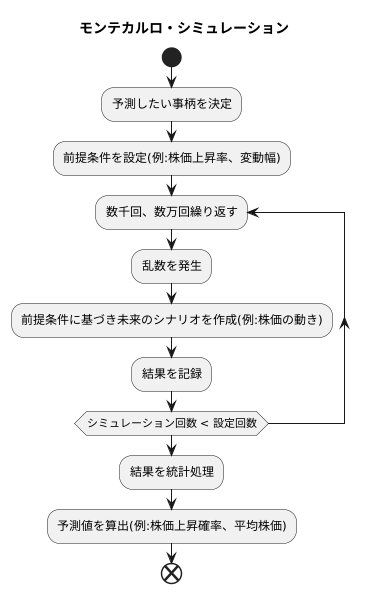
モンテカルロ・シミュレーションは、偶然の要素を含む不確かな未来を予測する有力な手法です。まるで無数の未来を覗き見て、全体像を把握しようとするかのようです。この手法は、名前の由来にもなったカジノで有名なモンテカルロから連想されるように、偶然性、すなわち乱数を用いる点が最大の特徴です。
まず、予測したい事柄について、いくつかの前提を定めます。例えば、株価の動きを予測したい場合、過去の株価の動きから、平均的な上昇率や変動の幅などを推定します。これらの値は、シミュレーションの土台となる重要な情報です。
次に、コンピュータを使って大量の乱数を発生させ、設定した前提条件に基づいて、様々な未来のシナリオを作り出します。株価の例で言えば、乱数を用いて、明日、明後日、そして1年後、2年後…の株価がどのように動くかを、何度も何度も計算していきます。1回ごとの計算結果は、ある特定の未来における株価の動きを示しています。
重要なのは、この計算を数千回、数万回と繰り返すことです。一度の計算では、たまたま極端な結果が出てしまう可能性もありますが、何万回も繰り返すことで、起こりうる様々な結果を網羅的に捉えることができます。そして、それぞれの結果を統計的に処理することで、例えば「株価が上がる確率」「予想される平均株価」といった予測値を算出することが可能になります。まるで無数の平行世界を覗き見て、未来を予測するような手法と言えるでしょう。
手法の利点と限界

「モンテカルロ・シミュレーション」とは、複雑な問題を解く際に、何度も何度もさいころを振るように乱数を用いて答えを予測する方法です。数式で表すのが難しい、あるいは解くのが大変な問題でも、この方法を使えばおおよその答えを導き出すことができます。
この手法の最大の強みは、複雑な事柄を比較的簡単に調べられることです。例えば、天気や株価の動きなど、様々な要因が複雑に絡み合って変化する現象を予測する際に役立ちます。いくつもの仮説を立て、それぞれの場合でどうなるかをシミュレーションすることで、将来起こりうる様々な状況を想定し、不確かな事態に対する備えをすることができます。
しかし、この手法には限界もあります。まず、シミュレーションを行う際に、いくつかの前提条件を設定する必要があります。例えば、過去のデータに基づいて将来の株価の動きを予測する場合、過去の傾向が今後も続くという前提を置くことになります。しかし、この前提が間違っていれば、シミュレーションの結果も信頼できません。つまり、前提条件の良し悪しが結果の良し悪しを大きく左右するのです。
もう一つの限界は、計算に時間がかかる場合があることです。特に、複雑な問題を扱う場合や、高い精度を求める場合は、膨大な量の計算が必要になります。そのため、高性能な計算機が必要になることもあります。
このようにモンテカルロ・シミュレーションには利点と限界がありますが、その特徴を正しく理解し、適切に用いることで、様々な場面で意思決定を助ける強力な道具となります。
| 項目 | 内容 |
|---|---|
| 定義 | 乱数を用いて何度も試行を繰り返すことで、複雑な問題の答えを予測する手法 |
| メリット | 複雑な事象を比較的簡単に分析できる。 様々な要因が絡み合う現象の予測に役立つ。 複数の仮説を検証し、将来の不確実性への備えができる。 |
| デメリット | 結果が前提条件の妥当性に大きく依存する。 複雑な問題や高精度を求める場合は計算に時間がかかる場合がある。 |
| 結論 | 利点と限界を理解し適切に用いれば、意思決定を支援する強力なツールとなる。 |
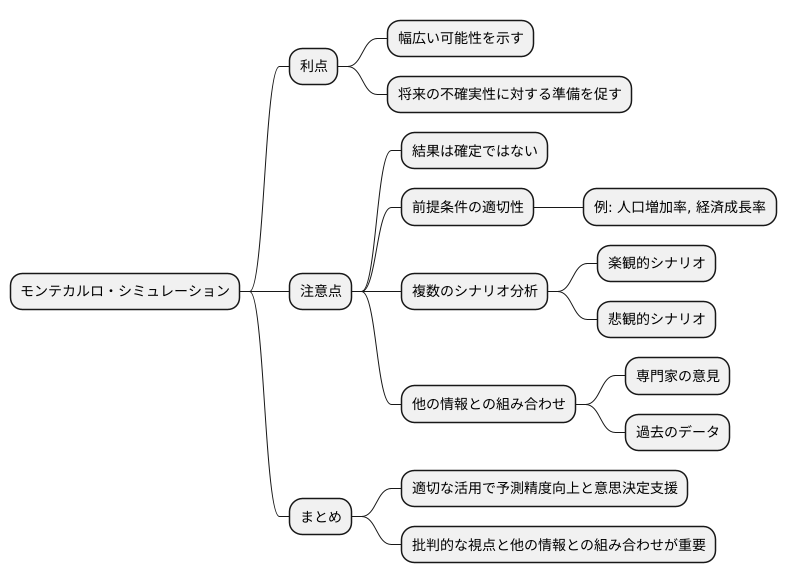
より良い未来予測のために

将来の展望をより確かなものにするために、様々な予測方法が存在しますが、その中でモンテカルロ・シミュレーションは有力な手段の一つです。この手法は、乱数を用いて何度も試行を繰り返すことで、起こりうる未来の可能性を幅広く示してくれます。しかし、ここで注意すべきは、シミュレーションはあくまでも可能性を示すものであり、その結果が確実に実現するとは限らないということです。
シミュレーションの結果をそのまま信じて行動するのではなく、結果が持つ意味を深く理解し、将来に潜む不確実性に対する準備をすることが重要です。そのためには、まずシミュレーションの前提となる条件が適切かどうかを注意深く検討する必要があります。例えば、人口増加率や経済成長率といった前提条件が現実と乖離していると、シミュレーションの結果も信頼性に欠けるものとなります。
また、様々な状況を想定し、複数のシナリオを分析することも重要です。楽観的なシナリオだけでなく、悲観的なシナリオも検討することで、想定外の事態が発生した場合にも対応できる柔軟な計画を立てることができます。さらに、シミュレーションの結果は単独で判断するのではなく、他の入手可能な情報、例えば専門家の意見や過去のデータなどと組み合わせて総合的に判断することで、より精度の高い予測が可能となります。
モンテカルロ・シミュレーションは、適切に活用することで、将来の予測精度を高め、より良い意思決定を支援する強力なツールとなります。しかし、その結果を盲信するのではなく、批判的な視点を持って解釈し、他の情報と組み合わせて活用することが、より良い未来を築く鍵となるでしょう。